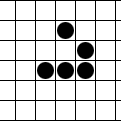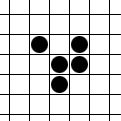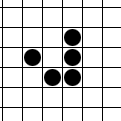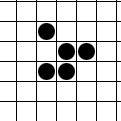
Згаданий раніше парадокс Каррі здобув популярність завдяки старанням популяризатора науки Мартіна Гарднера . Він же, як з’ясувалося, просував у маси гру “Життя” Джона Конвея. Побачивши цю назву, я тут же згадав… ¦Років 20 тому, коли жодними ноутбуками та інтернетами в моєму житті ще й не пахло, я вже намагався розважатися за допомогою електроніки. Точніше за допомогою Електроніки МК52 – програмованого калькулятора з дисплеєм на десяток розрядів.
На додаток до калькулятора батьки купили мені картридж БРП-4 з набором програм. Насамперед мене звичайно цікавили ігри. Всього 20-30 хвилин програмування та заповнення якихось там осередків пам’яті і ось по екрану біжать цифри. Це “Посадка на Місяць” – гра спеціально для осіб із багатою уявою. На екрані після тривалих обчислень з’являється три числа – поточне прискорення та висота та запас палива. Ти думаєш, і вводиш у відповідь два своїх числа – тривалість і потужність включення гальмівного ракетного двигуна. Калькулятор знову думає (близько хвилини). Завдання – плавно приземлиться, не пробивши Місяць наскрізь, або навпаки не відлетіти з орбіти.Так ось, однією з ігор, на картриджі було те саме “Життя” Конвея. Грати в неї без відповідного графічного відображення виявилося непосильним завданням для моєї дитячої уяви. Однак ідея саморозвивається штучної спільноти або багатоклітинного організму мені сподобалася і, як бачите, запам’яталася:
- Кожна клітина може знаходитися в одному з двох станів: жива (заповнена) або мертва (порожня).
- Кожен хід кожної клітини визначається її стан і стан всіх її 8-ми сусідів.
- Якщо це порожня клітина та сусідів рівно 3, то ця клітина оживає. У решті випадків порожня клітина залишається порожньою.
- Якщо це жива клітина, то підраховується кількість живих сусідів.
- Якщо сусідів 0 або 1, то клітина вмирає від самотності.
- Якщо сусідів 2 чи 3, то клітина продовжує жити.
- Якщо сусідів 4 або більше, то клітина вмирає від перенаселення.