Упомянутый ранее парадокс Карри получил известность благодаря стараниям популяризатора науки Мартина Гарднера. Он же, как выяснилось, продвигал в массы игру «Жизнь» Джона Конвея. Увидев это название, я тут же вспомнил… Лет 20 назад, когда никакими ноутбуками и интернетами в моей жизни еще и не пахло, я уже пытался развлекаться при помощи электроники. Точнее при помощи Электроники МК52 — программируемого калькулятора с дисплеем на десяток разрядов.
В дополнение к калькулятору родители купили мне картридж БРП-4 с набором программ. В первую очередь меня конечно интересовали игры. Всего 20-30 минут программирования и заполнения каких-то там ячеек памяти и вот по экрану бегут цифры. Это «Посадка на Луну» — игра специально для лиц с богатым воображением. На экране после длительных вычислений появляется три числа — текущее ускорение и высота и запас топлива. Ты думаешь, и вводишь в ответ два своих числа — длительность и мощность включения тормозного ракетного двигателя. Калькулятор снова думает (около минуты). Задача — плавно приземлится, не пробив Луну насквозь, или наоборот не улететь с орбиты.
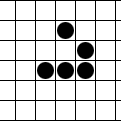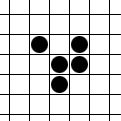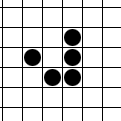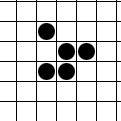
Так вот, одной из игр, на картридже была та самая «Жизнь» Конвея. Играть в нее без соответсвующего графического отображения оказалось задачей непосильной для моего детского воображения. Однако идея саморазвивающегося искусственного сообщества или многоклеточного организма мне понравилась и, как видите, запомнилась:
- Каждая клетка может находиться в одном из двух состояний: живая (заполненная) или мёртвая (пустая).
- Каждый ход у каждой клетки определяется ее состояние и состояние всех её 8-ми соседей.
- Если это пустая клетка и соседей ровно 3, то эта клетка оживает. Во всех остальных случаях пустая клетка остается пустой.
- Если же это живая клетка, то подсчитывается количество живых соседей.
- Если соседей 0 или 1, то клетка умирает от одиночества.
- Если соседей 2 или 3, то клетка продолжает жить.
- Если соседей 4 или больше, то клетка умирает от перенаселения.